Um exercício bastante simples permite imaginar melhor a diferença entre um número racional e um número irracional. Tal exercício consiste na fabricação de um número irracional chamado Φ partindo da sequência de Fibonacci.
Tal sequência deve seu nome ao matemático Leonardo Pisano, conhecido pelo pseudônimo de Fibonacci (1175-1250). O ponto de partida da sequência pode fazer sorrir um analista já que se trata de calcular a reprodução de uma população de coelhos a partir do par “fundador”. É uma demanda concreta colocada por criadores de coelhos que leva à construção da sequência.
O que nos interessa é o resultado, que é o seguinte: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Cada número resultando da adição dos dois precedentes.
Com essa sequência de números, constroem-se frações do tipo p/q, com p e q inteiros, com cada número e seu antecessor: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, etc. Dito de outra forma, busca-se a “relação” entre cada número e seu antecessor.
Em um terceiro tempo, calcula-se o valor de cada uma dessas frações.
Ressaltemos que, partindo de números racionais (é o cálculo de uma fração), o número de decimais de cada resultado será a cada vez finito ou periódico. Por exemplo, o resultado de 13/8 é 1,625. O que significa que o número de decimais termina na cifra 5. Seguindo a antiga técnica de verificação, se multiplicarmos 1,625 por 8, reencontraremos 13.
O número exato de decimais pode variar, mas estão, a cada vez, em quantidade finita ou periódica, mesmo que as calculadoras nem sempre permitam visualizá-los todos. Por exemplo, 5 dividido por 3 terá uma série infinita de 6. E 21/13 terá uma periodicidade de decimais 615384 615384…, tal como 34/21, 619047 619047…
A figura 7 apresenta três colunas com a série de Fibonacci, as frações e os resultados das frações.
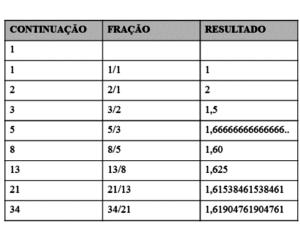
Figura 7.
A etapa seguinte consiste em inscrever esses números numa reta.
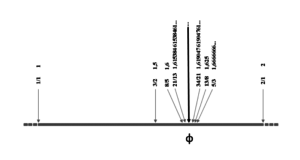
Figura 8. Sequência sobre a reta
Os resultados transpostos vão alternar ora para a direita, ora para a esquerda, em um ponto que vai se tornando preciso à medida que se avança na sequência.
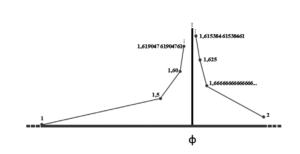
Figura 9. Sequência sobre um plano
Se inscrevermos esses valores obtidos sobre um plano de coordenadas cartesianas, veremos aparecer uma espécie de funil em torno de uma linha inacessível cercada, porém, de um lado e do outro. Esta linha corresponde a Φ, um número irracional que se desenvolve com a linha reta mostrando que é inacessível. Ele é inacessível porque infinito em sua escrita. Não cessa de se escrever, seus decimais nunca terminam, enquanto que aqueles que constituem as linhas em funil constituem números racionais, na íntegra. Eles terminam de se escrever. Essa figura mostra a diferença entre os números racionais, em cinza claro, e um irracional, em cinza escuro.
A propriedade de não poder se escrever inteiramente é a de todos os números irracionais. A série infinita de decimais constitui um muro que separa dois mundos, o dos números a sua esquerda e o dos números a sua direita. Dedekind chamou-o de corte.
Insistamos no fato de que, contrariamente aos números que o delimitam, um irracional comporta um número infinito de decimais. Assim, uma construção a partir de números racionais que resultam de uma razão ou proporção (rapport) entre dois números, permite visualizar o furo de um número irracional: um ponto cercado de um lado e do outro da reta. No grafo, duas curvas o delimitam sem jamais atingi-lo, e não sem motivo: a quantidade infinita e a priori imprevisível de decimais cria um fosso absolutamente intransponível.
Eis os primeiros decimais de Φ:
1,618033988749894848204586834365638117… Os três pontos indicam que a sequência de números continua ao infinito. Podemos dizer assim que um corte é produzido por um número irracional sobre a reta dos reais.
Esse procedimento inverte o sentido que se dava até então aos irracionais. É difícil dar um estatuto matemático a um elemento que não pode terminar de se escrever. E, no entanto, sua existência é atestada desde a Antiguidade.
Devemos lembrar que o número irracional faz furo ou corte e que este furo ou corte é delimitado por números racionais que dele se aproximam cada vez mais sem jamais atingi-lo. Insistamos em que por sua quantidade infinita de decimais, um irracional define uma fronteira, chamada em matemática limite, aquela que separa dois campos: o conjunto dos números que o precedem e o dos que o seguem.
Voltemos agora à psicanálise. Os números racionais (os que resultam das razões ou frações) permitem visualizar, nesse esquema, aquilo que é da ordem do significante.
Os significantes – as palavras enquanto unidades de sentido isoladas numa cadeia falada – funcionam como inteiros naturais. Tentam captar o objeto com palavras e, ao fazê-lo, eles delimitam um furo, o furo deixado pelo objeto perdido que, embora perdido, parece desencadear sua busca por meio da linguagem. O significante reporta-se à ordem dos “discretos”, como os números discretos, que vem de discretus, que quer dizer separado[1]. São unidades distintas umas das outras. Como os números racionais, os significantes rodeiam um furo, mesmo estando ordenados por uma função. Essa função que, no melhor dos casos, ordena ou põe ordem naquilo que pode ser dito é o que a psicanálise chama a função fálica[2].
Um objeto, o objeto a, deve ser situado no lugar do furo delimitado por unidades discretas.
Falta um significante para nomear o que foi a inscrição primeira, mas a estrutura psíquica busca reencontrá-lo no mecanismo de repetição que o caracteriza, sem jamais poder atingi-lo. Com efeito, o próprio da fala é que uma palavra não é nunca igual a si mesma. Um número irracional ilustra logicamente essa dimensão de inatingível que aparece com a efetivação da fala. Sua propriedade o torna apto a dar conta do objeto perdido freudiano e, mais especificamente, do objeto a de Lacan. Uma estrutura matemática permite dar conta do fato de que os significantes possam encontrar-se assim tão “imantados”.
Para a sequência de Fibonacci, a ordem vem das regras de sua construção.
Para o discurso analítico, o sujeito é impelido a existir por significantes que se desdobram tal como derivam as razões a partir de um axioma inicial de Fibonacci. A subjetividade é como tal criativa: ela se extenua ao produzir-se como significante a partir de uma verdade fundamental que não pode ser totalmente dita.
Duas noções principais podem expandir esta convergência para um irracional.
Por um lado, o infinito atual (ℵ0), cardinal dos inteiros, é um limite para o qual convergem os inteiros naturais. É usado por Lacan para designar a entrada do significante no Real. Dito de outra maneira, são as propriedades mesmas da ordem significante que inserem um primeiro significante inominável, o falo. Inominável, ele não aparece na cadeia sonora. Encontra-se na borda de tudo que é “dizível” sem poder ser pronunciado.
O estabelecimento da função do pai assegura essa ordem. O sujeito que se engaja na via da enunciação e do desejo gira em torno de uma nominação latente[3]. O furo de um irracional é “ocupado” por esse significante impronunciável graças ao qual todos os outros representam o sujeito. Em outras palavras, a função do pai faz desse furo o lugar de ocultação de um significante que ordena o sentido.
Mas essa mesma lógica dá conta da busca racional para cercar o objeto a que Lacan associa a um número irracional. E, aqui, o furo é o lugar do objeto e não um significante que o ocupe.
A novidade do discurso analítico é a de conceber a subjetividade de uma maneira diferente daquela de um discurso de mestria que se afirma a partir de um saber constituído e previsível. Um saber constituído visa a tamponar esse furo.
“O sujeito, em minha lógica, extenua-se ao se produzir como efeito do significante, permanecendo tão distinto deste, é claro, quanto um número real de uma sequência cuja convergência é assegurada racionalmente[4].”
Nosso esquema é uma sequência convergente que se aproxima do número Φ, cuja borda é construída racionalmente pelas frações iniciais. Já o dissemos acima, é a noção matemática de limite[5]. O irracional designa um lugar graças a uma letra (π, √2 , Φ) cuja ex-sistência pode ser racionalmente designada por aquilo que está em torno.
Em outras palavras, o sujeito procura dizer-se com palavras racionais que convergem para algo que lhe permanece exterior e inatingível, um número real – vemos aqui um irracional. Mas a lógica em jogo em R permite afirmar que ele o encontra no infinito[6].
Isso pode servir para descrever do que se trata no gozo sexual: os parceiros só se encontram no infinito, como Lacan sugere. Com efeito, a lógica implicada em R permite afirmar que a série infinita que limita um irracional equivale ao próprio irracional. Em outras palavras, π, √2 , Φ são subconjuntos do conjunto R .
Tais questões, de aparência árida, encontram um sentido analítico inesperado ao aclarar o sexo e o gozo. Um homem e uma mulher podem ser levados assim pela fala a um ponto para além das palavras, no infinito onde seus gozos podem se encontrar.
“Aquiles, é claro, só pode ultrapassar a tartaruga; não pode alcançá-la. Mas ele só a encontra no infinito. Aí está o dito para o que concerne ao gozo enquanto sexual[7]”.
*Capítulo do livro De Pitágoras a Lacan, uma história não oficial da Matemática para o uso dos psicanalistas, de autoria de Virginia Hasenbalg-Corabianu. O livro foi traduzido para circulação interna na AEPM e uso no dispositivo de leitura, coordenado por Livia Rocha e Maria Victoria Borges Díaz. Tradução: Periandro Ramos Barreto, Maria Victoria Borges Díaz, Maria Sílvia Antunes Furtado e Maria Virginia Moreira Guilhon. Título original: Hasenbalg-Corabianu, Virginia. De Pythagore à Lacan, une histoire non officielle des mathématiques à l’usage des psychanalystes. Éditions érès, 2016.
[1] Ver nota 1, p. 39.
[2] Procuraremos mais adiante apresentar “matematicamente” a noção de falo.
[3] M. Darmon, Essais sur la topologie lacanienne, AFI.
[4] Lacan, J. Le Séminaire, livre XIX, ...ou pire, lição de 10 de maio 1972.
Nota do tradutor: Na tradução para o português do livro 19 …ou pior, do Campo Freudiano no Brasil, a lição correspondente está datada de 11 de maio de 1972.
[5] Henri Cesbron Lavau me faz lembrar que uma vez extraída essa lógica própria dos números irracionais, a de constituir limites, ela se torna aplicável aos racionais em R. Pode-se desde então construir cortes ou limites para os racionais também pelo fato de sua pertença ao conjunto dos reais. Tomemos, por exemplo, 1,99 1,999 1,9999… e 2,01 2,001 2,0001… Essas duas sequências de números são também sequências convergentes para o número 2. A diferença é que um racional pode ser um limite para 1,99 1,999… 2 que, enquanto tal, será incluído na sequência. Naquele caso, não há mais lugar vazio. Então, quid o objeto a?
[6] Os racionais que circundam Φ, em nosso exemplo, são um subconjunto do conjunto R. A construção é feita sobre a reta dos reais.
[7] Lacan, J. Le Séminaire, livre XX, Encore, lição de 21 de novembro 1972.
Texto original em francês:
Un nombre irrationnel: comment le voir?
(Virginia Hasenbalg-Corabianu)
Un exercice assez simple permet de mieux imaginer la différence entre un nombre rationnel et un nombre irrationnel. Il consiste dans la fabrication d’un nombre irrationnel, appelé Φ en partant de la suite de Fibonacci.
Cette suite doit son nom au mathématicien italien Leonardo Pisano, connu sous le pseudonyme de Fibonacci (1175-1250). Le point de départ de la suite peut faire sourire un analyste puisqu’il s’agit de calculer la reproduction d’une population de lapins à partir d’un couple ”fondateur”. C’est une vraie demande posée par des éleveurs de lapins qui aboutit à la construction de la suite.
Ce qui nous importe, c’est le résultat, qui est le suivant: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Chaque nombre résultant de l’addition des deux précédents.
Avec cette suite de nombres, on construit des fractions du type p/q, avec p et q entiers, avec chaque nombre et son prédécesseur: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, etc. Autrement dit, on cherche le “rapport” entre chaque nombre et son prédécesseur.
Dans un troisième temps, on calcule la valeur de chacune de ces fractions.
Soulignons qu’en partant des nombres rationnels (c’est le calcul d’une fraction), le nombre de décimales de chaque résultat sera à chaque fois fini ou périodique. Par exemple, le résultat de 13/8 est 1,625. Ce qui signifie que le nombre de décimales s’arrête au chiffre 5. Suivant la veille technique de vérification, si on multiplie 1,625 par 8, on retrouve 13.
Le nombre exact de décimales peut varier, mais elles sont à chaque fois en quantité finie ou périodique, même si les calculatrices ne permettent pas toujours de toutes les visualiser. Par exemple 5 divisé par 3 aura une suite infinie de 6. Et 21/13 aura une périodicité de décimales 615384 615384…, ainsi que 34/21, 619047 619047…
Le tableau ci-dessous présente trois colonnes avec la suite de Fibonacci, les fractions e les résultats des fractions.
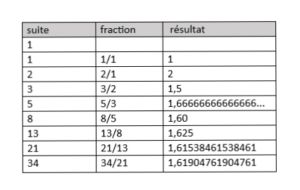
Figure 7.
L´étape suivante consiste à rapporter ces nombres sur une droite.

Figure 8. Suite sur la droite
Les résultats reportés vont alterner tantôt à droite, tantôt à gauche d’un point, qui se précise au fur et à mesure qu’on avance dans la suite.
 Figure 9. Suite sur un plan
Figure 9. Suite sur un plan
Si l’on reporte ces valeurs obtenues sur un plan de coordonnées cartésiennes, on voit apparaître une sorte d’entonnoir autour d’une ligne inaccessible mais cernée d’un côté et de l’autre. Cette ligne correspond à Φ, un nombre irrationel qui se déploie avec la ligne droite montrant qu’il est inaccessible. Il est inaccessible parce que infini dans son écriture. Il ne cesse pas de s’écrire, ses décimaux ne s’arrêtent jamais, alors que ceux qui constituent les lignes en entonnoir constituent des nombres rationnels à part entière: ils finissent de s’écrire. Cette figure montre la différence entre les nombres rationnels, en gris clair, et un irrationnel, en gris foncé.
Cette propriété de ne pas pouvoir s’écrire entièrement est celle de tous les nombres irrationnels. La suite infini de décimaux constitue un mur qui separe deux mondes, celui des nombres à sa gauche et celui des nombres à sa droite. Dedekind l’a nommé coupure.
Insistons sur le fait que, contrairement aux nombres qui le bornent, un irrationnel comporte un nombre infini de décimales. Ainsi, une construction à partir de nombres rationnels qui résultent d’un ratio, ou rapport entre deux nombres, permet de visualiser le trou d’un nombre irrationnel: un point cerné d’un côté et de l’autre de la droite. Dans le graphe, deux courbes le délimitent sans jamais l’atteindre, et pour cause: la quantité infinie et a priori imprévisible de décimales crée un fossé absolument infranchissable.
Voici les premières décimales de Φ:
1,618033988749894848204586834365638117… Les trois points indiquent que la suite de nombres continue à l’infini. On peut ainsi dire qu’une coupure est produite par un nombre irrationnel sur la droite des réels.
Ce procédé retourne le sens qu’on donnait jusqu’alors aux irrationnels. Il est difficile de donner un statut mathématique à un élément qui ne peut pas finir de s’écrire. Et pourtant leur existence est attestée depuis l’Antiquité.
C’est à retenir que le nombre irrationnel fait trou ou coupure, et ce trou ou coupure est bordé par des nombres rationnels qui l’approchent de plus en plus sans jamais l’atteindre. Insistons sur le fait que par sa quantité infinie de décimales, un irrationnel définit une frontière, appelée em mathématique limite, celle qui separe deux champs: l’ensemble des nombres qui le précèdent et celui de ceux qui le suivent.
Revenons alors à la psychanalyse. Les nombres rationnels (ceux qui résultent des ratios ou fractions) permettent de visualiser dans ce schéma ce qu’il en est de l’ordre du signifiant.
Les signifiants – les mots comme autant d’unités de sens isolés dans une chaîne parlée – fonctionnent comme des entiers naturels. Ils essaient de saisir l’ objet avec des mots, et en ce faisant ils bordent un trou, le trou laissé par l’objet perdu qui, bien que perdu, semble entraîner sa recherche par le langage. Le signifiant relève de l’ordre des “discrets”, comme les nombres discrets, qui vient de discretus, qui veut dire séparé[1]. Ce sont des unités distinctes les unes des autres. Comme les nombres rationnels, les signifiants bordent un trou, tout en étant ordonnés par une fonction. Cette fonction qui au meilleur des cas ordonne ou met de l’ordre dans ce qui peut être dit, c’est ce que la psychanalyse appelle la fonction phallique[2].
Un objet, l’objet a, est à situer à la place du trou bordé par des unités discrètes.
Un signifiant manque pour nommer ce qui fut l’inscription première, mais la structure psychique cherche à le retrouver dans le mécanisme de répétition qui le caractérise, sans pouvoir jamais l’atteindre. En effet, le propre de la parole est qu’un mot n’est jamais égal à lui-même. Un nombre irrationnel illustre logiquement cette dimension d’inatteignable qui apparaît avec la mise en place de la parole. Sa propriété le rend apte à rendre compte de l’objet perdu freudien, et plus spécifiquement de l’objet a de Lacan. Une structure mathématique permet de rendre compte du fait que les signifiants puissent se trouver ainsi “aimantés”.
Pour la suite de Fibonacci, l’ordre provient des règles de sa construction.
Pour le discours analytique, le sujet est poussé à exister par des signifiants qui se déploient comme découlent les ratios à partir d’un axiome de départ de Fibonacci. La subjectivité est à ce titre créative : elle s’exténue à se produire comme signifiant à partir d’une vérité fondamentale qui ne peut pas être dite totalement.
Deux notions majeures peuvent s’étayer sur cette convergence vers un irrationnel.
D’une part, l’infini actuel (ℵ0), cardinal des entiers, est une limite vers laquelle convergent les entiers naturels. Il est employé par Lacan pour désigner l’entrée du signifiant dans le Réel. Autrement dit, ce sont les propriétés mêmes de l’ordre signifiant qui mettent en place un premier signifiant innommable, le phallus. Innommable, il n’apparaît pas dans la chaîne sonore. Il se trouve au bord de tout ce qui est “dicible” sans pouvoir être prononcé.
La mise en place de la fonction du père assure cet ordre. Le sujet qui s’engage sur la voie de l’énonciation et du désir tourne autour d’une nomination latente[3]. Le trou d’un irrationnel est “occupé ” par ce signifiant imprononçable grâce auquel tous les autres représentent le sujet. Autrement dit, la fonction du père fait de ce trou le lieu de recel d’un signifiant imprononçable qui ordonne le sens.
Mais cette même logique rend compte de la quête rationnelle pour cerner l’objet a que Lacan associe à un nombre irrationnel. Et ici, le trou est le lieu de l’objet, et non pas un signifiant qui le colonise.
La nouveauté du discours analytique est de concevoir le subjectivité autrement que dans un discours de maîtrise qui s’affirme à partir d’un savoir constitué et prédictible. Un savoir constitué vise à boucher ce qu’il en est de ce trou.
“Le sujet, dans ma logique, s’exténue à se produire comme effet de signifiant, bien entendu en en restant aussi distinct qu’un nombre réel d’une suite dont la convergence est assurée rationnellement[4].”
Notre schéma est une suite convergente qui s’approche du nombre Φ, dont le bord est construit rationnellement par les fractions de départ. Nous l’avons dit plus haut, c’est la notion mathématique de limite[5]. L’irrationnel désigne une place grâce à une lettre (π, √2 , Φ) dont l’ex-sistence peut être rationnellement désignée par ce qui est autour.
Autrement dit, le sujet cherche à se dire avec des mots rationnels qui convergent vers quelque chose qui lui reste extérieur et inatteignable, un nombre réel – voyons ici un irrationnel. Mais la logique en jeu dans R permet d’affirmer qu’il le rejoigne à l’infini[6].
Cela peut servir à décrire ce qu’il en est de la jouissance sexuelle : les partenaires ne se rejoignent qu’à l’infini, comme le suggère Lacan. En effet, la logique impliquée dans R permet d’affirmer que la série infinie qui borde un irrationnel équivaut à l’irrationnel lui-même. Autrement dit, π, √2 , Φ sont des sous-ensembles de l’ensemble R .
Ces questiones d’apparence aride trouvent un sens analytique inattendu en éclairant le sexe et la jouissance. Un homme et une femme peuvent être amenés ainsi par la parole à un point au-delà des mots, dans l’infini où leurs jouissances peuvent se rencontrer.
“Achille, c’est bien clair, ne peut que dépasser la tortue, il ne peut pas la rejoindre. Mais il ne la rejoint que dans l’infinitude. Seulement en voilà de dit pour ce qui est de la jouissance, en tant qu’elle este sexuelle[7]“.
[1] Voir note 1, p. 47.
[2] On essaiera plus loin d’avancer “mathématiquement” sur la notion de phallus.
[3] M. Darmon. Essais sur la topologie lacanienne, AFI.
[4] J. Lacan, Le Séminaire, livre XIX, … ou pire, leçon du 10 mai 1972.
[5] Henri Cesbron Lavau me rappelle qu’une fois dégagée cette logique propre aux nombres irrationnels, celle de constituer des limites, elle devient applicable aux rationnels dans R. On peut dès lors construire des coupures ou limites pour les rationnels aussi, du fait de leur appartenance à l’ensemble des réels. Prenons par exemple 1,99 1,999 1,9999… et 2,01 2,001 2,0001… Ces deux suites de nombres sont aussi des suites convergentes vers le nombre 2. La différence est qu’un rationnel peut être aussi une borne 1,99 1,999… 2 qui en tant que telle sera incluse dans la suite. Dans ce cas-là, il n’y a plus de place vide. Alors, quid de l’objet a?
[6] Les rationnels qui bordent Φ dans notre exemple sont un sous-ensemble de R. La construction est faite sur la droite des réels.
[7] J. Lacan, Le Séminaire, livre XX, Encore, leçon du 21 novembre 1972.
